Coding Interview.

剑指Offer： https://leetcode.cn/problem-list/xb9nqhhg/
剑指Offer突击版： https://leetcode.cn/problem-list/e8X3pBZi/

Classification

LinkedList 6/18/22/23/24/25/35/52
Stack/Queue 9/30/31/58/59
Tree 7/8/26/27/28/32/33/34/36/37/54/55/68
Array 3/4/21/39/53/56
String 5/20/38/48/67
Heap 40
Hash Table 50
Graph/Backtracking 12/13
Fibonacci 10
Search 4/11/56
Sort 40/51
Full Permutation 38
Dynamic Programming 10/14/19/42
Bitwise Operation 15/16
Other 17/29/41/43/44/45/46/47/49/57/60/61/62/63/64/65/66

03.数组中的重复数字

03.1找出数组中重复的数字

题目描述

在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的，也不知道每个数字重复几次。请找出数组中任意一个重复的数字。

输入输出

Input:
{2，3，1，0，2，5，3}

Output:
2

大致思路

对于这种数组元素在 [0, n-1] 范围内的问题，可以将值为 i 的元素调整到第 i 个位置上进行求解。本题要求找出重复的数字，因此在调整过程中，如果第 i 位置上已经有一个值为 i 的元素，就可以知道 i 值重复。

java实现

public class Solution {
    // Parameters:
    //    numbers:     an array of integers
    //    length:      the length of array numbers
    //    duplication: (Output) the duplicated number in the array number,length of duplication array is 1,so using duplication[0] = ? in implementation;
    //                  Here duplication like pointor in C/C++, duplication[0] equal *duplication in C/C++
    //    这里要特别注意~返回任意重复的一个，赋值duplication[0]
    // Return value:       true if the input is valid, and there are some duplications in the array number
    //                     otherwise false
    public boolean duplicate(int numbers[],int length,int [] duplication) {
        int temp;
        if(length <= 0 || numbers == null)
            return false;
        for(int i = 0; i < length; i++){
            while(numbers[i] != i){
                if(numbers[i] != numbers[numbers[i]]){
                    temp = numbers[numbers[i]];
                    numbers[numbers[i]] = numbers[i];
                    numbers[i] = temp;
                }
                else{
                    duplication[0] = numbers[i];
                    return true;
                }
            }
        }
        return false;
    }
}

03.2不修改数组找出重复的数字

题目描述

在一个长度为 n + 1 的数组里的所有数字都在 1到 n 的范围内。数组中至少有一个数字重复，请找出任意一个重复的数字但不能修改输入的数组。

大致思路

利用二分法每次将1-n的数字分成1-m和m+1到n 若1-m的数字数目超过m则一定存在重复的数字否则 m+1到n存在重复数字接着再不断将两边区间继续二分直到找到一个重复数字

但无法保证找出所有重复数字 eg.1-2之间有两个2 这个范围数字也出现2次

04.二维数组中的查找

题目描述

给定一个二维数组，其每一行从左到右递增排序，从上到下也是递增排序。给定一个数，判断这个数是否在该二维数组中。

输入输出

Consider the following matrix:
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.
Given target = 20, return false.

大致思路

该二维数组中的一个数，小于它的数一定在其左边，大于它的数一定在其下边。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

java实现

//大致思路的实现
class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return false;
        int row = matrix.length,column = matrix[0].length;
        int r = 0,c = column - 1;
        while (r <= row-1 && c >= 0){
            if (matrix[r][c] == target)
                return true;
            else if(matrix[r][c] > target)
                c--;
            else
                r++;
        }
        return false;
    }
}

//牛客网只有这样才能ac 其实是一样的道理
public class Solution {
    public boolean Find(int target, int [][] array) {
        for(int i=0;i<array.length;i++){
            for(int j=0;j<array[0].length;j++){
                if(target<array[0][0]){
                    return false;
                }
                else if(target>array[i][j]){
                    continue;
                }
                else if(target==array[i][j]){
                    return true;
                }
            }
        }
        return false;
    }
}

05.替换空格

题目描述

将一个字符串中的空格替换成 “%20”。

输入输出

Input:
"A B"

Output:
"A%20B"

大致思路

O(n²)解法：
- 用指针从前往后扫描一碰到空格就把后边字符往后移两位插入%20
- 假设字符串长度为n 对每个空格字符需要移动后边的O(n)个字符因此对于含有O(n)个空格字符的字符串而言总时间效率O(n²)
O(n)解法：
- 用两个指针先申请好足够的空间(Space + 2*n n是空格数量) 使用前后两个指针遍历 p1在句子末尾 p2在空间末尾
- 依次复制字符串内容直到p1碰到空格 p2处即插入%20 然后再往前
- 先遍历一次字符串求空格数量再用双指针从后往前遍历总时间效率O(n)
以下代码使用了：String放在StringBuffer里操作最后在转换回来

java实现

class Solution {
    public String replaceSpace(String s) {
        StringBuffer sb = new StringBuffer();
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == ' ') {
                sb.append("%20");
                continue;
            }
            sb.append(s.charAt(i));
        }
        return sb.toString();
    }
}

06.从尾到头打印链表

题目描述

从尾到头反过来打印出每个结点的值。

输入输出

1 2	输入：head = [1,3,2] 输出：[2,3,1]

大致思路

利用栈顺序push之后再pop / 利用递归 / 利用头插法 link

java实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
//利用栈的结构先入后出
class Solution {
public int[] reversePrint(ListNode head) {
        if (head == null){
            return new int[0];
        }
        Stack<Integer> stack = new Stack<>();
        //所有值入栈
        while (head != null){
            stack.push(head.val);
            head = head.next;
        }
        //取得长度，本来喜欢直接调size()的，但是出栈会减小
        int n = stack.size();
        int[] ans = new int[n];
        //一个个的填充就好
        for (int i = 0;i < n;i ++ ){
            ans[i] = stack.pop();
        }
        return ans;
    }
}

//利用递归逆序把链表添加到ArrayList中
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        ArrayList<Integer> res = new ArrayList<>();
        if (listNode == null) {
            return res;
        }
        addElement(listNode, res);
        return res;
    }
    
    private void addElement(ListNode listNode, ArrayList<Integer> res) {
        if (listNode.next != null) {
            // 递归调用
            addElement(listNode.next, res);
        }
        res.add(listNode.val);
    }
}

//不用ArrayList的直接递归
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode subListHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return subListHead;
    }
}

//利用头插法
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null){
            return null;
        }
        ListNode p1 = head;
        ListNode p2 = head.next;
        p1.next = null;
        while(p2 != null){
            ListNode temp = p2.next;
            p2.next = p1;
            p1 = p2;
            p2 = temp;
        }
        return p1;
    }
}

07.重建二叉树

题目描述

根据二叉树的前序遍历和中序遍历的结果，重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

输入输出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回
    3
   / \
  9  20
    /  \
   15   7

大致思路

前序遍历的第一个值为根节点的值，使用这个值将中序遍历结果分成两部分，左部分为树的左子树中序遍历结果，右部分为树的右子树中序遍历的结果。然后分别对左右子树递归地求解。

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder.length == 0 || inorder.length == 0) {
            return null;
        }
        int n = preorder.length;
        return constructBinaryTree(preorder, 0, n - 1, inorder, 0, n - 1);
    }

    private TreeNode constructBinaryTree(int[] pre, int startPre, int endPre, int[] in, int startIn, int endIn) {
        TreeNode node = new TreeNode(pre[startPre]);
        if (startPre == endPre) {
            if (startIn == endIn) {
                return node;
            }
            throw new IllegalArgumentException("Invalid input!");
        }

        int inOrder = startIn;
        while (in[inOrder] != pre[startPre]) {
            ++inOrder;
            if (inOrder > endIn) {
                new IllegalArgumentException("Invalid input!");
            }
        }
        int len = inOrder - startIn;
        if (len > 0) {
            // 递归构建左子树
            node.left = constructBinaryTree(pre, startPre + 1, startPre + len, in, startIn, inOrder - 1);
        }

        if (inOrder < endIn) {
            // 递归构建右子树
            node.right = constructBinaryTree(pre, startPre + len + 1, endPre, in, inOrder + 1, endIn);
        }
        return node;

    }
}

// leetcode主题库用上述提交会超时
// 解决方法是在查找inorder[]的根节点时利用HashMap
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        int m = inorder.length;        
        if(m == 0 || m == 0 || m != n){
            return null;
        }

        Map<Integer, Integer> indexMap = new HashMap<>(n);
        for(int i = 0; i < n; i++){
            indexMap.put(inorder[i], i);
        }
        return constructTree(preorder, 0, n-1, indexMap, 0, n-1);
    }

    private TreeNode constructTree(int[] pre, int startPre, int endPre,
                                    Map<Integer, Integer> indexMap, int startIn, int endIn){
        if(startPre > endPre || startIn > endIn){
            return null;
        }
        
        int rootval = pre[startPre];
        TreeNode node = new TreeNode(rootval);
        int rootIndex = indexMap.get(rootval);
        node.left = constructTree(pre, startPre+1, rootIndex-startIn+startPre, indexMap, startIn, rootIndex-1);
        node.right = constructTree(pre, rootIndex-startIn+startPre+1, endPre, indexMap, rootIndex+1, endIn);
        return node;
    }
}

08.二叉树的下一个结点

题目描述

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

大致思路

该结点有右子树则是其右子树的最左节点
该结点无右子树

2.1 若他是一个左孩子则是其父

2.2 若他是一个右孩子则一直追溯其祖先直到是左子其父就是

java实现

/*
public class TreeLinkNode {
    int val;
    TreeLinkNode left = null;
    TreeLinkNode right = null;

    next指针指向其父结点
    TreeLinkNode next = null;

    TreeLinkNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode){
        if(pNode == null){
            return null;
        }
        
        if(pNode.right != null){
            TreeLinkNode node = pNode.right;
            while(node.left != null){
                node = node.left;
            }
            return node;
        }
        else{
             while(pNode.next != null){
                 TreeLinkNode parent = pNode.next;
                 if(parent.right != pNode){
                     return parent;
                 }
                 pNode = pNode.next;
             }
        }
        return null;
    }
}

09.栈和队列的实现

09_1 用两个栈实现队列

题目描述

用两个栈来实现一个队列，完成队列的 Push 和 Pop 操作。队列中的元素为 int 类型。

大致思路

牛客网

push:

把数据push进S1

pop:

若S2空S1不空把S1pop出来push进S2

若S2空S1不空报错

把S2pop出来

leetcode

appendTail: //务必让新元素放在S1栈底

若S1非空将S1全部pop出来 push进S2

把新的push进S1

若S2非空将S2全部pop出来push进S1

size+1

deleteHead:

若size==0 返回-1

若size>0 size– 再把S1pop出来

java实现

//牛客网
import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop(){
        if(stack2.isEmpty()){
            if(stack1.isEmpty()){
                return -1;
            }
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

//leetcode-cn
class CQueue {
    Stack<Integer> stack1;
    Stack<Integer> stack2;
    int size;

    public CQueue() {
        stack1 = new Stack<Integer>();
        stack2 = new Stack<Integer>();
        size = 0;
    }
    
    public void appendTail(int value) {
        while (!stack1.isEmpty()) {
            stack2.push(stack1.pop());
        }
        stack1.push(value);
        while (!stack2.isEmpty()) {
            stack1.push(stack2.pop());
        }
        size++;
    }
    
    public int deleteHead() {
        if (size == 0) {
            return -1;
        }
        size--;
        return stack1.pop();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
*/

09_2 用队列实现栈

题目描述

使用队列实现栈的下列操作：
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空

注意:
你只能使用队列的基本操作– 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

大致思路

使用辅助队列思想大致相同

java实现

class MyStack {
    Queue<Integer> queue;
    Queue<Integer> help_queue;

    /** Initialize your data structure here. */
    public MyStack() {
        queue = new LinkedList<>();
        help_queue = new LinkedList<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue.add(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        while(queue.size() > 1){
            help_queue.add(queue.poll());
        }
        int result = queue.poll();
        while(!help_queue.isEmpty()){
            queue.add(help_queue.poll());
        }
        return result;
    }
    
    /** Get the top element. */
    public int top() {
        while(queue.size() > 1){
            help_queue.add(queue.poll());
        }
        int result = queue.poll();
        help_queue.add(result);
        while(!help_queue.isEmpty()){
            queue.add(help_queue.poll());
        }
        return result;
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

10.斐波那契数列

题目描述

大致思路

java实现

//递归 O(2^n)
public class Solution {
    public int Fibonacci(int n) {
            if(n < 2){
                return n;
            }
            return Fibonacci(n-1)+Fibonacci(n-2);
    }
}

//保存中间数据 O(n)
class Solution {
    public int fib(int n) {
        if(n<2){
            return n;
        }
        int[] res =new int[n+1];
        res[0] = 0;
        res[1] = 1;
        for(int i=2; i<=n; ++i){
            res[i] = res[i-1] + res[i-2];
        }
        return res[n];
    }
}

//leetcode-cn要求用动态规划才能ac 待补坑

//变态跳台阶
public class Solution {
    public int JumpFloorII(int target) {
        if(target <= 2){
            return target;
        }
        else{
            return JumpFloorII(target - 1) * 2;
        }
    }
}

//矩形覆盖
public class Solution {
    public int RectCover(int target) {
        if(target <= 2){
            return target;
        }
        int[] res = new int[target+1];
        res[1] = 1;
        res[2] = 2;
        for(int i = 3; i<=target; i++){
            res[i] = res[i-1] + res[i-2];
        }
        return res[target];
    }
}

11.旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

输入输出

例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

大致思路

利用一个二分法提取一个中间指针不断缩小范围

java实现

//牛客网 需考虑index1 == index2 == indexMid的情况
class Solution {
    public int minArray(int[] numbers) {
        if(numbers.length <= 0){
            return 0;
        }
        int index1 = 0;
        int index2 = numbers.length -1;
        int indexMid = index1;
        while(numbers[index1] >= numbers[index2]){
            if(index2 - index1 == 1){
                indexMid = index2;
                break;
            }


            indexMid = (index1 + index2)/2;

            if(numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1]){
                return minInorder(numbers, index1, index2);
            }


            if(numbers[indexMid] <= numbers[index2]){
                index2 = indexMid;
            }
            else if(numbers[indexMid] >= numbers[1]){
                index1 = indexMid;
            }
        }
        return numbers[indexMid];
    }
    
    
    private int minInorder(int[] nums,int index1, int index2){
        int result = nums[index1];
        for(int i = index1 + 1;i <= index2; ++i){
            if(result > nums[i]){
                result = nums[i];
            }
        }
        return result;
    }

}

//leetcode超简单大牛方法 仅使用指针移动
class Solution {
    public int minArray(int[] numbers) {
        int i = 0,j = numbers.length - 1;
        while(i < j){
            int m = (i + j) / 2;
            if(numbers[m] > numbers[j])
                i = m + 1;
            else if(numbers[m] < numbers[j])
                j = m;
            else j--;
        }
        return numbers[i];
    }
}

12.矩阵中的路径

题目描述

判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

大致思路

使用回溯法（backtracking）进行求解，它是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。

java实现

//牛客网ac
public class Solution {
    /**
     * 判断字符矩阵是否包含某一个字符序列
     * @param matrix    
     * @param rows  矩阵行数
     * @param cols  矩阵列数
     * @param str   目标字符序列
     * @return
     */
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
        boolean visitFlags[] = new boolean[matrix.length];
        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {
                if (hasPathCore(matrix, rows, cols, row, col, str, 0, visitFlags))
                    return true;
            }
        }

        return false;
    }

    /**
     * 回溯法递归实现判断
     * @param matrix    字符矩阵
     * @param rows  矩阵行数
     * @param cols  矩阵列数
     * @param row   当前行索引
     * @param col   当前列索引
     * @param str   目标字符序列
     * @param k 目标字符序列中当前字符索引
     * @param visitFlags    字符矩阵是否被访问过标记
     * @return
     */
    boolean hasPathCore(char[] matrix, int rows, int cols, int row, int col, char[] str,  int k, boolean[] visitFlags) {
        int index = row * cols + col;
        // 行列索引超限、当前字符已经被访问过、当前字符不等于目标字符序列的当前字符，直接返回false
        if (row < 0 || col < 0 || row >= rows || col >= cols || 
                visitFlags[index] || matrix[index] != str[k])
            return false;

        visitFlags[index] = true;   // 设置访问标记
        if (k == str.length - 1)    // 递归结束条件，k已经到达目标字符序列的最后一个字符
            return true;

        k++;    // 匹配目标字符序列的下一个字符

        // 在当前字符的上、下、左、右的元素搜索下一个目标字符，递归
        if (hasPathCore(matrix, rows, cols, row + 1, col, str, k, visitFlags) || 
                hasPathCore(matrix, rows, cols, row - 1, col, str, k, visitFlags) || 
                hasPathCore(matrix, rows, cols, row, col + 1, str, k, visitFlags) || 
                hasPathCore(matrix, rows, cols, row, col - 1, str, k, visitFlags))
            return true;

        // // 在当前字符的上、下、左、右的元素没有搜索到下一个目标字符，将访问标记重置为false，返回false；
        visitFlags[index] = false;
        return false;
    }
}

//leetcode-cn 参数不同
class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for(int i = 0; i < board.length; i++) {
            for(int j = 0; j < board[0].length; j++) {
                if(dfs(board, words, i, j, 0)) return true;
            }
        }
        return false;
    }
    boolean dfs(char[][] board, char[] word, int i, int j, int k) {
        if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k])
            return false;
        if(k == word.length - 1)
            return true;
        char tmp = board[i][j];//值暂存在tmp中
        board[i][j] = '/';//访问过的位置内容改为/
        boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || 
                      dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
        board[i][j] = tmp;//恢复值
        return res;
    }
}

13.机器人的运动范围

题目描述

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

大致思路

回溯法+深度优先搜索

java实现

public class Solution {
    public int movingCount(int threshold, int rows, int cols) {
        if (threshold < 0 || rows < 1 || cols < 1) {
            return 0;
        }
        boolean[] visited = new boolean[rows * cols];
        return getCount(threshold, 0, 0, rows, cols, visited);
    }

    private int getCount(int threshold, int i, int j, int rows, int cols, boolean[] visited) {
        if (check(threshold, i, j, rows, cols, visited)) {
            visited[i * cols + j] = true;
            return 1
                    + getCount(threshold, i - 1, j, rows, cols, visited)
                    + getCount(threshold, i + 1, j, rows, cols, visited)
                    + getCount(threshold, i, j - 1, rows, cols, visited)
                    + getCount(threshold, i, j + 1, rows, cols, visited);
        }
        return 0;
    }

    private boolean check(int threshold, int i, int j, int rows, int cols, boolean[] visited) {
        return i >= 0
                && i < rows
                && j >= 0
                && j < cols
                && !visited[i * cols + j]
                && getDigitSum(i) + getDigitSum(j) <= threshold;
    }

    private int getDigitSum(int i) {
        int res = 0;
        while (i > 0) {
            res += i % 10;
            i /= 10;
        }
        return res;
    }
}

14. 剪绳子

题目描述

给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]xk[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

输入输出

1 2	输入：8 输出：18(233)

大致思路

动态规划：
不停地将问题分割变小

贪心算法：
尽可能多剪长度为 3 的绳子，并且不允许有长度为 1 的绳子出现。如果出现了，就从已经切好长度为 3 的绳子中拿出一段与长度为 1 的绳子重新组合，把它们切成两段长度为 2 的绳子。

证明：当 n >= 5 时，3(n - 3) - n = 2n - 9 > 0，且 2(n - 2) - n = n - 4 > 0。因此在 n >= 5 的情况下，将绳子剪成一段为 2 或者 3，得到的乘积会更大。又因为 3(n - 3) - 2(n - 2) = n - 5 >= 0，所以剪成一段长度为 3 比长度为 2 得到的乘积更大。

java实现

//动态规划
public class Solution {
    public int cutRope(int target) {
        if(target < 2){
            return 0;
        }
        if(target == 2){
            return 1;
        }
        if(target == 3){
            return 2;
        }
        int[] products = new int[target + 1];
        products[0] = 0; products[1] = 1; products[2] = 2; products[3] = 3;
        int max = 0;
        for(int i = 4; i <= target; i++){
            max = 0;
            for(int j = 1;j <= i/2; j++){
                int product = products[j] * products[i-j];
                if(max < product){
                    max = product;
                    products[i] = max;
                }
            }
        }
        return products[target];
    }
}

//贪婪算法
public class Solution {
    public int cutRope(int target) {
        if(target < 2){
            return 0;
        }
        if(target == 2){
            return 1;
        }
        if(target == 3){
            return 2;
        }
        int timesOf3 = target / 3;
        if(target - timesOf3 * 3 == 1){
            timesOf3--;
        }
        int timesOf2 = (target - timesOf3 * 3) / 2;
        return (int)(Math.pow(3, timesOf3)) * (int)(Math.pow(2, timesOf2));
    }
}

15.二进制中1的个数

题目描述

输入一个整数，输出该数二进制表示中 1 的个数。

大致思路

把一个整数减一并与它原来本身相与能够把最右边的一位1变成0

以上操作可以做几次则原数字中有多少个1

java实现

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        while(n != 0){
            ++count;
            n = (n - 1) & n;
        }
        return count;
    }
}

16.数值的整数次方

题目描述

给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent，求 base 的 exponent 次方。

大致思路

1.当指数为负时取其绝对值算出结果之后取倒数

2.用公式将次方分割成奇数和偶数再用递归逐步分割

java实现

//function1
public class Solution {
    public double Power(double base, int exponent) {
        double result = 1.0;
        int n = Math.abs(exponent);
        for(int i = 0; i < n; i++){
            result *= base;
        }
        return exponent<0? 1.0/result: result;
  }
}

//function2
class Solution {
    public double myPow(double x, int n) {
        long num = n;
        return pow(x, num);
    }
    
    private double pow(double x, long n){
        if(n == 0)
            return 1;
        if(n == 1)
            return x;
        boolean isNegative = false;
        if(n < 0){
            n = -n;
            isNegative = true;
        }
        double pow_result = pow(x * x, n / 2);
        if(n % 2 != 0){
            pow_result *= x;
        }
        return isNegative?1 / pow_result: pow_result;
    }
}

17.打印从1到最大的n位数

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

输入输出

1 2	输入：3 输出：0-999

大致思路

print1ToMaxOfNDigits用于将每一位从1加到9

printNumber用于将每一位打印出来（注：遇到099时从第二位开始打印）

java实现

//原书中的解法
public void print1ToMaxOfNDigits(int n) {
    if (n <= 0)
        return;
    char[] number = new char[n];
    print1ToMaxOfNDigits(number, 0);
}

private void print1ToMaxOfNDigits(char[] number, int digit) {
    if (digit == number.length) {
        printNumber(number);
        return;
    }
    for (int i = 0; i < 10; i++) {
        number[digit] = (char) (i + '0');
        print1ToMaxOfNDigits(number, digit + 1);
    }
}

private void printNumber(char[] number) {
    int index = 0;
    while (index < number.length && number[index] == '0')
        index++;
    while (index < number.length)
        System.out.print(number[index++]);
    System.out.println();
}

//leetcode简化了
class Solution {
    public int[] printNumbers(int n) {
        int max = (int)Math.pow(10, n);
        int[] ans = new int[max - 1];
        for(int i = 1 ; i <= max - 1 ; i++){
            ans[i - 1] = i;
        }
        return ans;
    }
}

18.删除链表的节点

18.1删除链表节点(给定指针)

题目描述

O(1)时间删除链表节点

大致思路

将节点的值赋值给他的前一个节点再修改next指针

java实现

public ListNode deleteNode(ListNode head, ListNode tobeDelete) {
    if (head == null || tobeDelete == null)
        return null;
    if (tobeDelete.next != null) {
        // 要删除的节点不是尾节点
        ListNode next = tobeDelete.next;
        tobeDelete.val = next.val;
        tobeDelete.next = next.next;
    } else {
        if (head == tobeDelete)
             // 只有一个节点
            head = null;
        else {
            ListNode cur = head;
            while (cur.next != tobeDelete)
                cur = cur.next;
            cur.next = null;
        }
    }
    return head;
}

18.2删除链表中的节点(给定值)

输入输出

输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

大致思路

还是双指针

java实现

class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        if(head.val == val) return head.next;
        ListNode pre = head, cur = head.next;
        while(cur != null && cur.val != val) {
            pre = cur;
            cur = cur.next;
        }
        pre.next = cur.next;
        return head;
    }
}

18.3删除链表中重复的节点

输入输出

1 2	输入：1->2->3->3->4->4->5 输出：1->2->5

大致思路

设置两个指针pre和cur pre指向cur的前一个指针 cur过虑重复值

java实现

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
//常规
public class Solution {
    public ListNode deleteDuplication(ListNode pHead){
        if (pHead == null || pHead.next == null) {
            return pHead;
        }
        
        ListNode pre = null;
        ListNode cur = pHead;
        while (cur != null) {
            if (cur.next != null && cur.next.val == cur.val) {
                int val = cur.val;
                while (cur.next != null && cur.next.val == val) {
                    cur = cur.next;
                }
                if(pre == null){
                    //这个 if-else 用于考虑pre压根没有移动的情况 eg.[1,1,1,2]
                    pHead = cur.next;
                }
                else{
                    pre.next = cur.next;
                }
            } else {
                pre = cur;
            }
            cur = cur.next;
        }
        return pHead;
    }
}

//使用递归
public ListNode deleteDuplication(ListNode pHead) {
    if (pHead == null || pHead.next == null)
        return pHead;
    ListNode next = pHead.next;
    if (pHead.val == next.val) {
        while (next != null && pHead.val == next.val)
            next = next.next;
        return deleteDuplication(next);
    } else {
        pHead.next = deleteDuplication(pHead.next);
        return pHead;
    }
}

19.正则表达式匹配

题目描述

请实现一个函数用来匹配包含'. '和'*'的正则表达式。
模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。
在本题中，匹配是指字符串的所有字符匹配整个模式。
例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

输入输出

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

大致思路

def ideas():
    if(两串中有一串为空):
        return false;
    if(两串都遍历完):
        return true;
    if(模式串第二位是 * 时):
        if(模式串与字符串第一位相同 或 模式串第一位是 . ):
            递归比较(i,j+2) || (i+1,j) || (i+1,j+2);
        else:
            递归比较(i,j+2);
    if(模式串与字串的第一位相同 或 模式串第一位是 . ):
        递归比较(i+1,j+1);
    return false;

java实现

public class Solution {
public  boolean match(char[] str, char[] pattern)
{
        if(str == null || pattern == null){
            return false;
        }
        else{
            return match(str, 0, pattern, 0);
        }
}

private  boolean match(char[] str, int i, char[] pattern, int j) {
       if(j == pattern.length)//pattern遍历完了
            return str.length == i;//如果str也完了，返回true，不然false
       //注意数组越界问题，一下情况都保证数组不越界
       if(j < pattern.length - 1 && pattern[j + 1] == '*') {//下一个是*
           if(str.length != i && //当前匹配
                   (str[i] == pattern[j] || pattern[j] == '.')) //匹配
               return match(str,i,pattern,j + 2)
                       || match(str,i + 1,pattern,j)
                       || match(str,i + 1,pattern,j + 2);
           else//当前不匹配
               return match(str,i,pattern,j + 2);
       }
       //下一个不是“*”，当前匹配
       if(str.length != i && (str[i] == pattern[j] || pattern[j] == '.'))
           return match(str,i + 1,pattern,j + 1);
        return false;
    }
}

20.表示数值的字符串

题目描述

1
2
3

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）
例如，字串"+100"、"5e2"、"-123"、"3.1416"、"0123"及"-1E-16"都表示数值
但"12e"、"1a3.14"、"1.2.3"、"+-5"及"12e+5.4"都不是

大致思路

1 2	scanUnsignedInteger(): 判断有无0 ~ 9的数字 scanInteger(): 判断以+ 或 -起始的数字中是否有1 ~ 9的数字

java实现

//牛客网
public class Solution {
    
    private int index = 0;
    
    public boolean isNumeric(char[] str) {
        if (str == null || str.length < 1) {
            return false;
        }

        // 判断是否存在整数
        boolean flag = scanInteger(str);

        // 小数部分 让index指针走到小数点后一位
        if (index < str.length && str[index] == '.') {
            index++;
            // 小数部分可以有整数或者没有整数
            flag = scanUnsignedInteger(str) || flag;
        }

        if (index < str.length && (str[index] == 'e' || str[index] == 'E')) {
            index++;
            // 让index指针走到e 或 E后一位
            // e或E前面必须有数字 后面也必须有整数
            flag = scanInteger(str) && flag;
        }

        return flag && index == str.length;

    }

    private boolean scanInteger(char[] str) {
        // 去除符号
        if(index < str.length && (str[index] == '+' || str[index] == '-')) {
            index++;
        }
        return scanUnsignedInteger(str);
    }

    private boolean scanUnsignedInteger(char[] str) {
        int start = index;
        while (index < str.length && str[index] >= '0' && str[index] <= '9') {
            index++;
        }
        // 判断是否存在整数
        return index > start;
    }
}

//leetcode答案 设置boolean A,B,C 逻辑更加清晰

/*
核心: 有效数字的模式只有两种:
1)A[.[B]][e|EC]  比如: +100   -67.0  29.    3.14E5
2).B[e|EC]       比如: .3     .4E6
其中,A、C是整数，B是正整数; [e|EC]表示[eC]或者[EC]
原则: 有A的话,有没有B都可以; 没有A的话, 必须有B
*/

class Solution {
    //扫描字符串时的索引
    int i = 0;

    public boolean isNumber(String s) {
        //input check
        if (s == null || s.length() == 0)
            return false;
        //去掉首尾的空字符
        s = s.trim();
        //判断是否有A; 同时将B,C初始化为false
        boolean A = scanInteger(s), B = false, C = false;
        //判断是否有B; 使用索引时要确保索引不越界
        if (i < s.length() && s.charAt(i) == '.') {
            //i当前指向'.', 所以需要i++
            i++;
            B = scanUnsignedInteger(s);
        }
        //判断是否有C
        if (i < s.length() && (s.charAt(i) == 'e' || s.charAt(i) == 'E')) {
            i++;
            C = scanInteger(s);
            //如果存在e|E, 但是没有C, 说明不是数字
            if (C == false)
                return false;
        }
        //here, 说明C是合格的, 只需判断A和B的情况
        //i必须扫描完整个字符串 && (有A的话,有没有B都可以; 没有A的话, 必须有B)
        return i == s.length() && (A || B);

    }

    //扫描整数
    private boolean scanInteger(String s) {
        //判断是否有'+'或者'-'
        if (i < s.length() && (s.charAt(i) == '+' || s.charAt(i) == '-'))
            i++;
        //扫描正整数
        return scanUnsignedInteger(s);
    }

    //扫描正整数
    private boolean scanUnsignedInteger(String s) {
        //起始索引
        int start = i;
        while (i < s.length() && s.charAt(i) >= '0' && s.charAt(i) <= '9') {
            i++;
        }
        //i>start说明扫描到了数字; 
        //i<=start说明没有扫描到数字, 此种情况说明要么start越界, 要么s.charAt(start)不是数字
        return i > start;
    }
}

21.调整数组顺序使奇数位于偶数前面

题目描述

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分。
（加扩展）并保证奇数和奇数，偶数和偶数之间的相对位置不变。

大致思路

需要相对位置不变时用冒泡排序

java实现

//牛客网（加扩展）
public class Solution {
    public void reOrderArray(int[] nums) {
        int N = nums.length;
        for (int i = N - 1; i > 0; i--) {
            for (int j = 0; j < i; j++) {
                if (isEven(nums[j]) && !isEven(nums[j + 1])) {
                    swap(nums, j, j + 1);
                }
            }
        }
    }

    private boolean isEven(int x) {
        return x % 2 == 0;
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

//leetcode 不需要相对位置不变
class Solution {
    public int[] exchange(int[] nums) {
        int i = 0, j = nums.length - 1, tmp;
        while(i < j) {
            while(i < j && (nums[i] & 1) == 1) i++;
            while(i < j && (nums[j] & 1) == 0) j--;
            tmp = nums[i];
            nums[i] = nums[j];
            nums[j] = tmp;
        }
        return nums;
    }
}

22.链表中倒数第k个节点

题目描述

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有6个节点，从头节点开始，它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。

大致思路

双指针前后一起移动（注意代码的鲁棒性）

java实现

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindKthToTail(ListNode head,int k) {
        if(head == null || k == 0){
            return null;
        }
        
        //保证k小于链表长度
        int length = 0;
        ListNode count = head;
        while(count != null){
            count = count.next;
            length++;
        }
        if(k > length){
            return null;
        }
        
        
        ListNode p1 = head;
        while(k-- > 0 && p1 != null){
            p1 = p1.next;
        }
        ListNode p2 = head;
        while(p1 != null){
            p2 = p2.next;
            p1 = p1.next;
        }
        
        return p2;
    }
}

23.链表中环的入口节点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

大致思路

先利用快慢指针。若能相遇，说明存在环，且相遇点一定是在环上；若没有相遇，说明不存在环，返回 null。
固定当前相遇点，用一个指针继续走，同时累积结点数。计算出环的结点个数 cnt。
指针 p1 先走 cnt 步，p2 指向链表头部，之后 p1,p2 同时走，相遇时，相遇点一定是在环的入口处。因为 p1 比 p2 多走了环的一圈。

java实现

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead)
    {
        if(pHead == null || pHead.next == null){
            return null;
        }
        
        //判断是否是环
        ListNode fast = pHead;
        ListNode slow = pHead;
        boolean isLoop = false;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            if(fast == slow){
                isLoop = true;
                break;
            }
        }
        if(!isLoop){
            return null;
        }
        
        ListNode cur = slow.next;
        int count = 1;
        while(cur != slow){
            cur = cur.next;
            count++;
        }
        
        ListNode p1 = pHead;
        while(count > 0){
            p1 = p1.next;
            count--;
        }
        
        ListNode p2 = pHead;
        while(p1 != p2){
            p1 = p1.next;
            p2 = p2.next;
        }
        return p2;
    }
}

24.反转链表

题目描述

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

输入输出

1 2	输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL

大致思路

递归 or 双指针迭代

java实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */

//递归
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode newHead = reverseList(head.next);
        //例如，1，2，3，4，5,null
        //current是5
        //head是4
        //head.next 是 5
        //head.next.next 就是5指向的指针，指向当前的head（4）
		//5-4-3-2-1-null
        head.next.next = head;
        //注意把head.next设置为null，切断4链接5的指针
        head.next = null;
        //每层递归返回当前的节点，也就是最后一个节点。
        //（因为head.next.next改变了，所以下一层current变4，head变3）
        return newHead;
    }
}

//双指针迭代
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;
        ListNode temp = null;
        while(cur != null){
            temp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }
}

25.合并两个排序的链表/数组

题目描述

（数组）给定两个排序后的数组 A 和 B，其中 A 的末端有足够的缓冲空间容纳 B。编写一个方法，将 B 合并入 A 并排序。初始化 A 和 B 的元素数量分别为 m 和 n。

大致思路

merge 常规套路

java实现

//数组
class Solution {
    public void merge(int[] A, int m, int[] B, int n) {
        int i = m - 1;
        int j = n - 1;
        int k = m + n - 1;
        while(i >= 0 && j >= 0){
            if(A[i] > B[j]){
                A[k--] = A[i--];
            }
            else{
                A[k--] = B[j--];
            }
        }
        while(j >= 0){
            A[k--] = B[j--];
        }
    }
}

//链表 用递归 注释的是去掉重复元素
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1 == null)
            return l2;
        if(l2 == null)
            return l1;
        ListNode head = null;
        if(l1.val <= l2.val){
            //head = l1;
            //head.next = mergeTwoLists(l1.next, l2);
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else{
            //head = l2;
            //head.next = mergeTwoLists(l1, l2.next);
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
        //return head;
    }
}

//链表 非递归
public class Solution {
    /**
     * 合并两个排序链表
     * @param list1 链表1
     * @param list2 链表2
     * @return 合并后的单调不递减链表
     */
    public ListNode Merge(ListNode list1, ListNode list2) {
        if (list1 == null) {
            return list2;
        }
        if (list2 == null) {
            return list1;
        }

        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;
        ListNode p1 = list1;
        ListNode p2 = list2;
        while (p1 != null && p2 != null) {
            if (p1.val < p2.val) {
                ListNode t = p1.next;
                cur.next = p1;
                p1.next = null;
                p1 = t;
            } else {
                ListNode t = p2.next;
                cur.next = p2;
                p2.next = null;
                p2 = t;
            }
            //cur会走到最后 eg.[1,2,3] [4,5]走到3处
            cur = cur.next;
        }
        cur.next = p1 == null ? p2 : p1;
        return dummy.next;
    }
}

26.树的子结构

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

输入输出

例如:
给定的树 A:

     3
    / \
   4   5
  / \
 1   2
给定的树 B：

   4 
  /
 1
返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

大致思路

1 2	isAhasB()查找A中是否有和B一样的节点R isSubStructure()查找A中以R为根节点的子树是不是和B一样结构

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(A == null || B == null){
            return false;
        }
        return isAhasB(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    //isAhasB()查找A中是否有和B一样的节点R
    //isSubStructure()查找A中以R为根节点的子树是不是和B一样结构
    
    private boolean isAhasB(TreeNode A, TreeNode B){
        if(B == null){
            return true;
        }
        if(A == null){
            return false;
        }
        if(A.val != B.val){
            return false;
        }
        return isAhasB(A.left, B.left) && isAhasB(A.right, B.right);
    }
}

27.二叉树的镜像

题目描述

操作给定的二叉树，将其变换为源二叉树的镜像。

输入输出

二叉树的镜像定义：源二叉树 
    	    8
    	   /  \
    	  6   10
    	 / \  / \
    	5  7 9 11
    	镜像二叉树
    	    8
    	   /  \
    	  10   6
    	 / \  / \
    	11 9 7  5

大致思路

递归

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null){
            return null;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }
}

28.对称的二叉树

题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

输入输出

输入：root = [1,2,2,3,4,4,3]
输出：true
输入：root = [1,2,2,null,3,null,3]
输出：false

大致思路

1	一棵树的前序遍历等于他对称树的反前序遍历(根右左)

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return isSymmetric(root, root);
    }

    public boolean isSymmetric(TreeNode pRoot1, TreeNode pRoot2){
        if(pRoot1 == null && pRoot2 == null){
            return true;
        }
        if(pRoot1 == null || pRoot2 == null){
            return false;
        }
        if(pRoot1.val != pRoot2.val){
            return false;
        }
        
        return isSymmetric(pRoot1.left, pRoot2.right) && isSymmetric(pRoot1.right, pRoot2.left);
    }
}

29.顺时针打印矩阵

题目描述

4乘4 的矩阵数字从1到16 顺时针打印

输入输出

矩阵顺时针打印结果为：1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10

大致思路

先左到右再上到下再右到左再下到上

java实现

//牛客网
public ArrayList<Integer> printMatrix(int[][] matrix) {
    ArrayList<Integer> ret = new ArrayList<>();
    int r1 = 0, r2 = matrix.length - 1, c1 = 0, c2 = matrix[0].length - 1;
    while (r1 <= r2 && c1 <= c2) {
        for (int i = c1; i <= c2; i++)
            ret.add(matrix[r1][i]);
        for (int i = r1 + 1; i <= r2; i++)
            ret.add(matrix[i][c2]);
        if (r1 != r2)
            for (int i = c2 - 1; i >= c1; i--)
                ret.add(matrix[r2][i]);
        if (c1 != c2)
            for (int i = r2 - 1; i > r1; i--)
                ret.add(matrix[i][c1]);
        r1++; r2--; c1++; c2--;
    }
    return ret;
}

//leetcode大佬
class Solution {
    public int[] spiralOrder(int[][] matrix) {
        int m = matrix.length;
        if(m==0){
            return new int[]{};
        }
        int n = matrix[0].length;
        int top = 0, bot = m-1, left = 0, right = n-1;      //设置上下左右界限
        int cnt = 0;
        int[] res = new int[m*n];

        while(top<=bot&&left<=right){                       //遍历matrix
            for(int j=left;j<=right;j++){                   //从左到右
                res[cnt++] = matrix[top][j];
            }
            top++;
            for(int i=top;i<=bot;i++){                      //从上到下
                res[cnt++] = matrix[i][right];
            }
            right--;
            for(int j=right;j>=left&&top<=bot;j--){         //从右到左
                res[cnt++] = matrix[bot][j];
            }
            bot--;
            for(int i=bot;i>=top&&left<=right;i--){         //从下到上
                res[cnt++] = matrix[i][left];
            }
            left++;
        }
        return res;
    }
}

30.包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

输入输出

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

大致思路

设置两个栈一个存数据一个存最小值保证后者栈顶是当前栈内数据的最小值

java实现

//牛客网
import java.util.Stack;
public class Solution {

    private Stack<Integer> dataStack = new Stack<>();
    private Stack<Integer> minStack = new Stack<>();
    public void push(int node) {
        dataStack.push(node);
        minStack.push(minStack.isEmpty()? node: Math.min(minStack.peek(), node));
    }
    
    public void pop() {
        dataStack.pop();
        minStack.pop();
    }
    
    public int top() {
        return dataStack.peek();
        //peek()和pop()的区别在于他取栈顶的值 但不删掉
    }
    
    public int min() {
        return minStack.peek();
    }
}

//leetcode 着重于pop()时保持两个栈元素的一致性
class MinStack {

    /** initialize your data structure here. */
    Stack<Integer> dataStack,minStack;
    
    public MinStack() {
        dataStack = new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int x) {
        dataStack.add(x);
        if(minStack.isEmpty() || x <= minStack.peek()){
            minStack.add(x);
        }
    }
    
    public void pop() {
        if(dataStack.pop().equals(minStack.peek())){
            minStack.pop();
        }
    }
    
    public int top() {
        return dataStack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

31.栈的压入弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

输入输出

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false

大致思路

取一个栈模拟操作如果有弹出序列中的元素则pop 如果最后栈为空则序列正确

java代码

import java.util.Stack

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        for(int num : pushed){
            stack.push(num);
            while(!stack.isEmpty() && stack.peek() == popped[i]){
                stack.pop();
                i++;
            }
        }
        return stack.isEmpty();
    }
}

32.从上往下打印二叉树

32.1从上往下打印二叉树

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。（层次遍历）

输入输出

三层满二叉树输出1 2 3 4 5 6 7

大致思路

层次遍历

java实现

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        ArrayList<Integer> ret = new ArrayList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int count = queue.size();
            while(count-- > 0){
                TreeNode t = queue.poll();
                if(t == null){
                    continue;
                }
                ret.add(t.val);
                queue.add(t.left);
                queue.add(t.right);
            }
        }
        return ret;
    }
}

32.2 从上到下打印二叉树

题目描述

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

输入输出

分行打印

大致思路

设置变量按每层打印完循环一次打印一次设置一个tmp存储新的数据

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null)
            queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--){
                TreeNode t = queue.poll();
                tmp.add(t.val);
                if(t.left != null)
                    queue.add(t.left);
                if(t.right != null)
                    queue.add(t.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

32.3按之字形顺序打印二叉树

题目描述

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

大致思路

层序遍历+双端队列/两个栈/直接用变量标记奇数行偶数行用Collections反转保存

java实现

//采用第三种方法
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root != null)
            queue.add(root);
        boolean reverse = false;
        while(!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<>();
            int cnt = queue.size();
            while(cnt-- > 0){
                TreeNode node = queue.poll();
                if(node == null)
                    continue;
                list.add(node.val);
                queue.add(node.left);
                queue.add(node.right);
            }
            if(reverse)
                Collections.reverse(list);
            reverse = !reverse;
            if(!list.isEmpty())
                res.add(list);

        }
        return res;
    }
}

33.二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

输入输出

     5
    / \
   2   6
  / \
 1   3
输入: [1,6,3,2,5]
输出: false
输入: [1,3,2,6,5]
输出: true

大致思路

后序遍历中最后一个值是根节点可分割前边节点值为小于他和大于他两部分在这个情况下继续不断递归划分

java实现

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence == null || sequence.length == 0)
            return true;
        return verify(sequence, 0, sequence.length - 1);
    }
    
    private boolean verify(int[] sequence, int first, int last){
        if(last - first <= 1)
            return true;
        int rootval = sequence[last];
        int index = first;
        while(index < last && sequence[index] <= rootval){
            index++;
        }
        for(int i = index; i < last; i++){
            if(sequence[i] < rootval)
                return false;
        }
        return verify(sequence, first, index-1) && verify(sequence, index, last-1);
    }
}

34.二叉树中和为某一值的路径

题目描述

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

输入输出

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

[
   [5,4,11,2],
   [5,8,4,5]
]

大致思路

前序遍历+回溯法设置path中数值和是否等于target 不能的话回溯到上一个结点访问其他子节点

java代码

//leetcode
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root, sum);
        return res;
    }

    private void recur(TreeNode root, int target){
        if(root == null)
            return;
        path.add(root.val);
        target -= root.val;
        if(root.left == null && root.right == null && target == 0)
            res.add(new LinkedList(path));
        recur(root.left, target);
        recur(root.right, target);
        path.removeLast();
    }
}

35.复杂链表的复制

题目描述

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针random指向一个随机节点），请对此链表进行深拷贝，并返回拷贝后的头结点。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

大致思路

1.先把所有链表节点再原始节点后边复制一遍

在复制出来的新节点上建立random连接

将链表拆分开来

2.使用HashMap键值对存储再连接

java实现

// function1
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}

class Solution {
    public Node copyRandomList(Node head) {
        if(head == null){
            return null;
        }
        copyNode(head);
        randomDirect(head);
        return reList(head);
    }

    // 复制节点
    private void copyNode(Node head){
        while(head != null){
            Node nextNode = head.next;
            Node newNode = new Node(head.val);
            head.next = newNode;
            newNode.next = nextNode;
            head = nextNode;
        }
    }

    // 节点建立random连接
    private void randomDirect(Node head){
        while(head != null){
            Node nextNode = head.next;
            if(head.random != null){
                Node direct = head.random;
                nextNode.random = direct.next;
            }
            head = nextNode.next;
        }
    }

    // 重新组成两条链表
    private Node reList(Node head){
        Node newNode = head.next;
        Node newHead = newNode;
        head.next = newNode.next;
        head = head.next;
        while(head != null){
            newNode.next = head.next;
            head.next = head.next.next;
            head = head.next;
            newNode = newNode.next;
        }
        return newHead;
    }

}

// function2
class Solution {
    public Node copyRandomList(Node head) {
        HashMap<Node, Node> hashmap = new HashMap<>();
        Node cur = head;
        // put
        while(cur != null){
            hashmap.put(cur, new Node(cur.val));
            cur = cur.next;
        }
        // get
        cur = head;
        while(cur != null){
            hashmap.get(cur).next = hashmap.get(cur.next);
            hashmap.get(cur).random = hashmap.get(cur.random);
            cur = cur.next;
        }
        return hashmap.get(head);
    }
}

36.二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

大致思路

二叉搜索树的中序遍历是递增序列
先中序遍历再设置双向链表的左右指针
最后设置第一个节点和最后一个节点的左右指针

java实现

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    Node pre, head;
    public Node treeToDoublyList(Node root) {
        if(root == null)
            return null;
        inOrder(root);
        head.left = pre;
        pre.right = head;
        return head;
    }
    public void inOrder(Node cur){
        if(cur == null)
            return;
        inOrder(cur.left);
        
        if(pre != null)
            pre.right = cur;
        else
            head = cur;
        cur.left = pre;
        pre = cur;

        inOrder(cur.right);
    }
}

39.数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

输入输出

1 2	输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2

大致思路

多数投票问题，可以利用 Boyer-Moore Majority Vote Algorithm 来解决这个问题，使得时间复杂度为 O(N)。

使用 cnt 来统计一个元素出现的次数，当遍历到的元素和统计元素相等时，令 cnt++，否则令 cnt–。如果前面查找了 i 个元素，且 cnt == 0，说明前 i 个元素没有 majority，或者有 majority，但是出现的次数少于 i / 2 ，因为如果多于 i / 2 的话 cnt 就一定不会为 0 。此时剩下的 n - i 个元素中，majority 的数目依然多于 (n - i) / 2，因此继续查找就能找出 majority。

java实现

class Solution {
    public int majorityElement(int[] nums) {
        int majority = nums[0];
        for(int i = 1, cnt = 1; i < nums.length; i++){
            cnt = nums[i] == majority?cnt + 1: cnt - 1;
            if(cnt == 0){
                cnt = 1;
                majority = nums[i];
            }
        }
        int cnt = 0;
        for(int value : nums){
            if(value == majority){
                cnt++;
            }
        }
        return cnt > (nums.length / 2) ? majority : 0; 
    }
}

40.最小的k个数

题目描述

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

大致思路

使用快速排序（注意找前 K 大/前 K 小问题不需要对整个数组进行 O(NlogN)O(NlogN) 的排序！
例如本题，直接通过快排切分排好第 K 小的数（下标为 K-1），那么它左边的数就是比它小的另外 K-1 个数啦～）
堆排序（java中有现成的 PriorityQueue ）
二叉搜索树
数量有限时直接计数排序
神仙BFPRT算法

java实现

//Solution 1 QuickSort
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if(k == 0 || arr.length == 0)
            return new int[0];
        return QuickSort(arr, 0, arr.length - 1, k-1);
    }

    private int[] QuickSort(int[] arr, int low, int high, int k){
        int pivot = partition(arr, low, high);
        if(pivot == k){
            return Arrays.copyOf(arr, pivot + 1);
        }
        return pivot < k? QuickSort(arr, pivot + 1, high, k) : QuickSort(arr,low, pivot - 1, k); 
    }

    private int partition(int[] nums, int low, int high){
        int pivot = nums[low];
        while(low < high){
            while(low < high && nums[high] >= pivot){
                --high;
            }
            nums[low] = nums[high];
            while(low < high && nums[low] <= pivot){
                ++low;
            }
            nums[high] = nums[low];
        }
        nums[low] = pivot;
        return low;
    }
}

//Solution 2 Heap
// 保持堆的大小为K，然后遍历数组中的数字，遍历的时候做如下判断：
// 1. 若目前堆的大小小于K，将当前数字放入堆中。
// 2. 否则判断当前数字与大根堆堆顶元素的大小关系，如果当前数字比大根堆堆顶还大，这个数就直接跳过；
//    反之如果当前数字比大根堆堆顶小，先poll掉堆顶，再将该数字放入堆中。
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // 默认是小根堆，实现大根堆需要重写一下比较器。
        Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
        for (int num: arr) {
            if (pq.size() < k) {
                pq.offer(num);
            } else if (num < pq.peek()) {
                pq.poll();
                pq.offer(num);
            }
        }
        
        // 返回堆中的元素
        int[] res = new int[pq.size()];
        int idx = 0;
        for(int num: pq) {
            res[idx++] = num;
        }
        return res;
    }
}

42.连续子数组的最大和

题目描述

输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

输入输出

1
2
3

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

大致思路

状态定义：设动态规划列表 dp，dp[i] 代表以元素nums[i]为结尾的连续子数组最大和。
- 为何定义最大和dp[i]中必须包含元素nums[i]：保证dp[i] 递推到dp[i+1]的正确性；如果不包含nums[i] ，递推时则不满足题目的连续子数组要求。
转移方程：若dp[i-1] ≤ 0 ，说明dp[i-1]对dp[i]产生负贡献那dp[i-1] + nums[i]还不如nums[i]本身大。
- 当 dp[i - 1] > 0时：执行dp[i] = dp[i-1] + nums[i] ；
- 当 dp[i - 1] <= 0时：执行 dp[i] = nums[i]；
初始状态： dp[0] = nums[0]，即以 nums[0]结尾的连续子数组最大和为 nums[0]。
返回值：返回 dp列表中的最大值，代表全局最大值。

java实现

class Solution {
    public int maxSubArray(int[] nums) {
        if(nums == null || nums.length == 0)
            return 0;
        int greatestSum = Integer.MIN_VALUE;
        int sum = 0;
        for(int value : nums){
            sum = sum < 0? value: sum + value;
            greatestSum = Math.max(greatestSum, sum);
        }
        return greatestSum;
    }
}

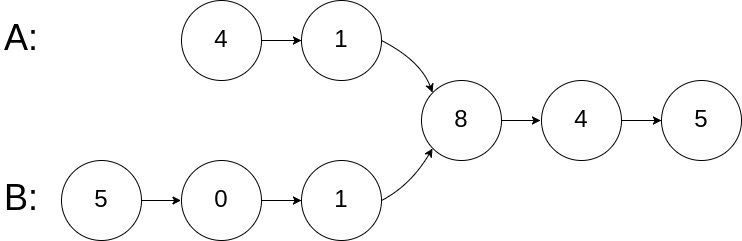
52.两个链表的第一个公共节点

题目描述

输入两个链表，找出它们的第一个公共节点。

输入输出

1
2
3

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

大致思路

双指针同时向后移动每当链表A上的指针走完就从B开始链表B上的指针走完就从A开始相遇节点=公共节点

java实现

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if(headA == null || headB == null){
            return null;
        }
        ListNode node1 = headA;
        ListNode node2 = headB;
        while(node1 != node2){
            node1 = node1 != null? node1.next: headB;
            node2 = node2 != null? node2.next:headA;
        }
        return node1;
    }
}

54.二叉搜索树的第k大节点

题目描述

给定一棵二叉搜索树，请找出其中第k大的节点。

输入输出

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

大致思路

递归解析：

终止条件：当节点 root 为空（越过叶节点），则直接返回；
递归右子树：即 dfs(root.right) ；
三项工作：
1. 提前返回：若k=0 ，代表已找到目标节点，无需继续遍历，因此直接返回；
2. 统计序号：执行 k=k−1 （即从 k 减至 0 ）；
3. 记录结果：若 k = 0 ，代表当前节点为第 k 大的节点，因此记录 res=root.val；
递归左子树：即dfs(root.left)；

java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int res,k;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return res;
    }

    void dfs(TreeNode root){
        if(root == null)
            return;
        dfs(root.right);
        if(k == 0)
            return;
        if(--k == 0)
            res = root.val;
        dfs(root.left);
    }
}

57.和为s的两个数字

57.1

题目描述

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

输入输出

1 2	输入：nums = [2,7,11,15], target = 9 输出：[2,7] 或者 [7,2]

大致思路

设置前后两个指针一个在数组首部一个在数组尾部两个值相加

若小于所求和则首部指针后移若大于所求和则尾部指针前移

java实现

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int i = 0, j = nums.length - 1;
        while(i < j) {
            int s = nums[i] + nums[j];
            if(s < target) i++;
            else if(s > target) j--;
            else return new int[] { nums[i], nums[j] };
        }
        return new int[0];
    }
}

57.2

题目描述

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大

输入输出

1 2	输入：target = 9 输出：[[2,3,4],[4,5]]

大致思路

当窗口的和小于 target 的时候，窗口的和需要增加，所以要扩大窗口，窗口的右边界向右移动
当窗口的和大于 target 的时候，窗口的和需要减少，所以要缩小窗口，窗口的左边界向右移动
当窗口的和恰好等于 target 的时候，我们需要记录此时的结果。设此时的窗口为 [i, j[i,j)，那么我们已经找到了一个 ii 开头的序列，也是唯一一个 ii 开头的序列，接下来需要找 i+1i+1 开头的序列，所以窗口的左边界要向右移动

java实现

//牛客网
import java.util.ArrayList;
public class Solution {
    public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
        ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
        
        int start = 1,end = 2;
        int curSum = 3;
        int middle = (1 + sum)/2;
        while(start < middle){
            if(curSum < sum){
                end++;
                curSum += end;
            }
            else if(curSum > sum){
                curSum -= start;
                start++;
            }
            else{
                ArrayList<Integer> list = new ArrayList<>();
                for(int i = start; i <= end; i++){
                    list.add(i);
                }
                ret.add(list);
                curSum -= start;
                start++;
                end++;
                curSum += end;
            }
        }
        return ret;
    }
}

//leetcode
public int[][] findContinuousSequence(int target) {
    int i = 1; // 滑动窗口的左边界
    int j = 1; // 滑动窗口的右边界
    int sum = 0; // 滑动窗口中数字的和
    List<int[]> res = new ArrayList<>();

    while (i <= target / 2) {
        if (sum < target) {
            // 右边界向右移动
            sum += j;
            j++;
        } else if (sum > target) {
            // 左边界向右移动
            sum -= i;
            i++;
        } else {
            // 记录结果
            int[] arr = new int[j-i];
            for (int k = i; k < j; k++) {
                arr[k-i] = k;
            }
            res.add(arr);
            // 左边界向右移动
            sum -= i;
            i++;
        }
    }

    return res.toArray(new int[res.size()][]);
}

59.队列的最大值

59.1滑动窗口的最大值

题目描述

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

输入输出

输入: nums = [1,3,-1,-3,5,3,6,7] 和 k = 3
输出: [3,3,5,5,6,7] 

  滑动窗口的位置                最大值

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

大致思路

使用双端队列进行操作(队列中不存值存数组下标)

java实现

//leetcode 返回数组
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || k < 1 || nums.length < k || nums.length == 0) {
            return new int[0];
        }

        int index = 0;
        int[] res = new int[nums.length - k + 1];
        LinkedList<Integer> qMax = new LinkedList<>();

        for (int i = 0; i < nums.length; i++) {
            // 在队列不为空的情况下，如果队列尾部的元素要比当前的元素小，或等于当前的元素
            // 那么为了维持从大到小的原则，我必须让尾部元素弹出
            while (!qMax.isEmpty() && nums[qMax.peekLast()] <= nums[i]) {
                qMax.pollLast();
            }
            // 不走 while 的话，说明我们正常在队列尾部添加元素
            qMax.addLast(i);
            // 如果滑动窗口已经略过了队列中头部的元素，则将头部元素弹出
            if (qMax.peekFirst() == (i - k)) {
                qMax.pollFirst();
            }
            // 看看窗口有没有形成，只有形成了大小为 k 的窗口，我才能收集窗口内的最大值
            if (i >= (k - 1)) {
                res[index++] = nums[qMax.peekFirst()];
            }
        }
        return res;
    }
}

//牛客网 返回ArrayList 原理相同
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size)
    {
        ArrayList<Integer> reList = new ArrayList<>();
        if (num == null || num.length < size || size < 1) {
            return reList;
        }

        Deque<Integer> deque = new LinkedList<>();
        for (int i = 0; i < num.length; i++) {

            // 队尾元素比要入队的元素小，则把其移除（因为不可能成为窗口最大值）
            while (!deque.isEmpty() && num[deque.getLast()] <= num[i]) {
                deque.pollLast();
            }
            // 队首下标对应的元素不在窗口内（即窗口最大值），将其从队列中移除
            while (!deque.isEmpty() && (i - deque.getFirst() + 1 > size)) {
                deque.pollFirst();
            }
            // 把每次滑动的值加入到队列中
            deque.add(i);
            // 滑动窗口的首地址i大于size就写入窗口最大值
            if (!deque.isEmpty() && i + 1 >= size) {
                reList.add(num[deque.getFirst()]);
            }
        }
        return reList;
    }
}

59.2队列的最大值

题目描述

请定义一个队列并实现函数 max_value 得到队列里的最大值
要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)

若队列为空，pop_front 和 max_value 需要返回 -1

输入输出

输入: 
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

输入: 
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出: [null,-1,-1]

大致思路

维护一个队列和双端队列

队列用于操作双端队列用于储存队首到队尾值从大到小

java代码

class MaxQueue {
    Queue<Integer> que;
    Deque<Integer> deq;

    public MaxQueue() {
        que = new LinkedList<>();  //队列：插入和删除
        deq = new LinkedList<>();  //双端队列：获取最大值
    }
    
    public int max_value() {
        return deq.size()>0?deq.peek():-1;  //双端队列的队首为que的最大值
    }
    
    public void push_back(int value) {
        que.offer(value);  //value入队
        while(deq.size()>0 && deq.peekLast()<value){
            deq.pollLast();  //将deq队尾小于value的元素删掉
        }
        deq.offerLast(value);  //将value放在deq队尾
    }
    
    public int pop_front() {
        //最后出队的状态必须保持原来队列
        //eg[4,2,0,3] [4,2,0,3]
        int tmp = que.size()>0?que.poll():-1;  //获得队首元素
        if(deq.size()>0 && tmp == deq.peek()){
            deq.poll();  //如果出队的元素是当前最大值，将deq的队首出队
        }
        return tmp;
    }
}

60.n个骰子的点数

题目描述

把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

输入输出

输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

大致思路

一个leetcode里不错的解析

java实现

class Solution {
    public double[] twoSum(int n) {
        double pre[]= {1/6d, 1/6d, 1/6d, 1/6d, 1/6d, 1/6d};
        for(int i = 2; i <= n; i++){
            double tmp[] = new double[5 * i + 1];
            for(int j = 0; j < pre.length; j++){
                for(int x = 0; x < 6; x++){
                    tmp[j+x] += pre[j] / 6;
                }
            }
            pre = tmp;
        }
        return pre;
    }
}

61.扑克牌中的顺子

题目描述

从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2～10为数字本身，A为1，J为11，Q为12，K为13，而大、小王为 0 ，可以看成任意数字。A 不能视为 14。

输入输出

输入: [1,2,3,4,5]
输出: True
输入: [0,0,1,2,5]
输出: True

大致思路

五张是顺子必须满足以下两个条件：

除大小王外，所有牌 无重复 ；
设此 55 张牌中最大的牌为 max ，最小的牌为 min （大小王除外），则需满足：

max - min < 5

Function1：集合Set+遍历
Function2：先对数组进行排序计算数组中0的个数存在joker中最后判断 nums[4] - nums[joker] < 5 ?

java实现

import java.util.Set;
import java.util.HashSet;

//Function1
class Solution {
    public boolean isStraight(int[] nums) {
        if(nums == null || nums.length == 0)
            return false;
        Set<Integer> repeat = new HashSet<>();
        int max = 0,min = 14;
        for(int num:nums){
            if(num == 0)
                continue;
            max = Math.max(num, max);
            min = Math.min(num, min);
            if(repeat.contains(num))
                return false;
            repeat.add(num);
        }
        return max - min < 5;
    }
}

//Function2
class Solution {
    public boolean isStraight(int[] nums) {
        int joker = 0;
        Arrays.sort(nums); // 数组排序
        for(int i = 0; i < 4; i++) {
            if(nums[i] == 0) joker++; // 统计大小王数量
            else if(nums[i] == nums[i + 1]) return false; // 若有重复，提前返回 false
        }
        return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
    }
}

63.圆圈中最后剩下的数字

题目描述

让小朋友们围成一个大圈。然后，随机指定一个数 m，让编号为 0 的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌，然后可以在礼品箱中任意的挑选礼物，并且不再回到圈中，从他的下一个小朋友开始，继续 0…m-1 报数 …. 这样下去 …. 直到剩下最后一个小朋友，可以不用表演。

输入输出

1 2	输入：n=5 m=3 输出：3

大致思路

代码使用循环的方法可反推回来计算：
只有1个人了，那个人就是获胜者，他的下标位置是0
在有2个人的时候，幸存者的下标位置为1
在有3个人的时候，幸存者的下标位置为1
在有4个人的时候，幸存者的下标位置为0

CSDN解析约瑟夫环(Josephus Problem)

java实现

//递归
public class Solution {
    public int LastRemaining_Solution(int n, int m) {
        if(n == 0)
            return -1;
        if(n == 1)
            return 0;
        return (LastRemaining_Solution(n - 1, m) + m ) % n;
    }
}

//循环
class Solution {
    public int lastRemaining(int n, int m) {
        int ans = 0;
        for(int i = 2; i <= n; i++){
            ans = (ans + m) % i;
        }
        return ans;
    }
}

64.求1+2+…+n

题目描述

求1+2+3+…+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

大致思路

使用递归解法最重要的是指定返回条件，但是本题无法直接使用 if 语句来指定返回条件。
条件与 && 具有短路原则，即在第一个条件语句为 false 的情况下不会去执行第二个条件语句。利用这一特性，将递归的返回条件取非然后作为 && 的第一个条件语句，递归的主体转换为第二个条件语句，那么当递归的返回条件为 true 的情况下就不会执行递归的主体部分，递归返回。
本题的递归返回条件为 n <= 0，取非后就是 n > 0；递归的主体部分为 sum += Sum_Solution(n - 1)，转换为条件语句后就是 (sum += Sum_Solution(n - 1)) > 0。
最后一个>0是因为&&本身就是判断语句必须返回boolean类型所以使用>0

java实现

public int Sum_Solution(int n) {
    int sum = n;
    boolean b = (n > 0) && ((sum += Sum_Solution(n - 1)) > 0);
    return sum;
}